그래프 탐색 알고리즘에 대한 이해가 선행되어야 한다. 그래프와 DFS/BFS의 개념을 모른다면 여기를 추천한다.
Depth-First Search (DFS)
- 저번 시간에 한 것📍
- 깊이 우선 탐색
- 이번 포스팅에서는 weigh을 가지지 않는 방향 그래프에서 모든 경우를 구해볼 때 이 DFS를 사용할 것이다. 예를 들면 1부터 N까지의 자연수 중 n개의 집합을 만들 수 있을 때, 가능한 모든 순열을 구해야 할 때 사용할 수 있다.
- 스택을 통해 구현한다. 즉, 재귀함수를 통해 구현할 것이다. (함수가 호출되면 스택 영역에 쌓이게 된다. 함수가 무한호출될 때 Stack Overflow 가 발생하는 것도 여기서 기인하는 것.)
Breadth-First Search (BFS)
- 이번 시간에 할 것📍
- 너비 우선 탐색
- 다음 포스팅에서 weigh을 가지지 않는 방향 그래프에서 최단/최소 경로를 구해볼 때 이 BFS를 사용할 것이다. 예를 들면 A노드(A도시)에서 B노드(B도시)로 가기 위해서는 어떤 edge들을 선택해 어떤 노드들을 거쳐가는 것이 최소 경로인가(어떤 버스를 선택해 어떤 도시를 경유하는 것이 최소환승이 될 수 있는가?)의 문제가 있다.
- 큐를 통해 구현한다.
실제로 문제를 한 번 풀어보자.
1부터 시작해 N개의 노드를 가지는 방향 그래프가 주어진다. 1번 노드에서 시작하여 2~N번 노드에 도달할 수 있는 최단 루트를 각각 구하시오.
- 입력: N을 위한 자연수 n과 edge들의 연결 정보를 위한 (i, j) 배열. (i번 노드에서 j번 노드로 이어지는 edge가 존재한다)
- 출력: 1번에서 출발해 2~N번 노드에 도달하는 최단 루트를 각각 출력
예를 들어 다음과 같은 입력이 주어진다고 치자.
- n: 6
- edge 정보: [(1,5), (2,4), (2,5), (3,2), (3,6), (4,2), (4,5), (5,3), (5,6)]
그러면 아래와 같은 방향 그래프가 만들어질 것이다.
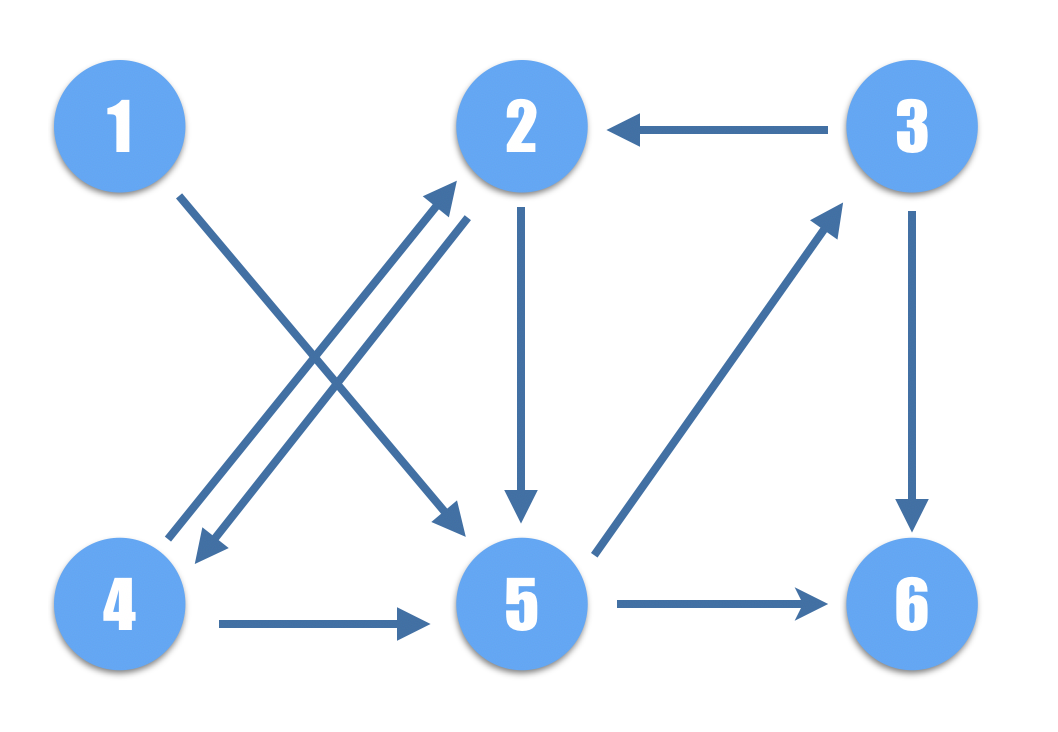
1번에서 출발하여 다른 노드들에 도달하는 최단 루트는 다음과 같다.
- 1 - 5 - 3 - 2
- 1 - 5 - 3
- 1 - 5 - 3 - 2 - 4
- 1 - 5
- 1 - 5 - 6
이것이 곧 기대 출력값이 된다.
이 최단 루트를 찾는 과정은 결국 1번 노드를 루트로 두는 방향 그래프에서, BFS를 이용해 MST(Minimum Spanning Tree)를 만드는 과정을 거치는 것이다.
이 과정을 간단히 그림으로 나열해보았다.




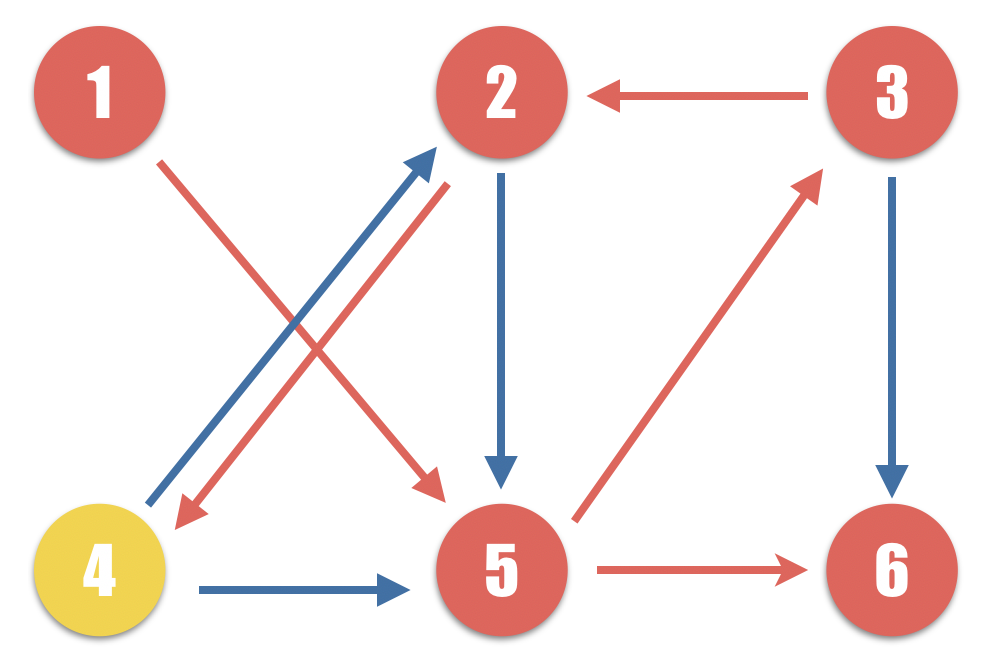


1번 노드에서 출발해서 2~N번 노드에 도달하는 최소 루트를 간단히 알 수 있게 된다.
이제 이것을 직접 코드로 구현해보자.
DFS 포스트에서는 Node나 Edge등의 자료구조 없이도 원리만 이해하고 있다면 문제를 해결할 수 있다는 것을 알아보았다. 이번에는 Node와 Edge 자료구조를 한 번 활용해보자.
class Node<T> {
let value: T
var edges = [Edge<T>]()
var visited = false
init(value: T) {
self.value = value
}
func appendEdgeTo(_ node: Node<T>) {
let edge = Edge<T>(from: self, to: node)
self.edges.append(edge)
}
}
class Edge<T> {
weak var source: Node<T>?
let destination: Node<T>
init(from source: Node<T>, to destination: Node<T>) {
self.source = source
self.destination = destination
}
}Node와 Edge를 간단히 만들어보았다.
이것들을 이용해 BFS로 문제를 풀어보자.
func practiceBFS(n: Int, edges: [(Int, Int)]) {
// Node, Edge setup
let nodes = (0..<n).map({ Node<Int>(value: $0 + 1) })
for (from, to) in edges {
nodes[from - 1].appendEdgeTo(nodes[to - 1])
}
// 1. 궁극적으로 원하는 값
var shortest = Array(repeating: [1], count: n)
var queue = Queue<Node<Int>>()
queue.enqueue(nodes[0])
nodes[0].visited = true
while let node = queue.dequeue() {
for edge in node.edges {
let dest = edge.destination
guard dest.visited == false else { continue }
queue.enqueue(dest)
dest.visited = true
// 2. Node를 방문할 때 해야하는 처리
shortest[dest.value - 1] = shortest[node.value - 1] + [dest.value]
}
}
print(shortest)
}
practiceBFS(n: 6, edges: [(1,5), (2,4), (2,5), (3,2), (3,6), (4,2), (4,5), (5,3), (5,6)])
// print "[[1], [1, 5, 3, 2], [1, 5, 3], [1, 5, 3, 2, 4], [1, 5], [1, 5, 6]]"포인트는 주석에 번호를 매겨놓은 두 부분이다.
- 1. 궁극적으로 원하는 값. BFS를 수행하며 우리가 찾고자 하는 결과. 여기서는 2~N번 노드까지의 최소 루트가 될 것이다. i번째 인덱스에 (i+1)번 노드까지의 최소 루트를 저장하는 배열을 선언하였다.
- 2. Node를 방문할 때 해야하는 처리. 중복되지 않게 노드를 방문할 때 해야할 처리이다. 여기서는 '다음 방문할 노드까지의 최소 거리' 에 '현재 노드를 오는 데까지의 루트' + '다음 방문할 노드의 번호'를 할당하는 처리를 하고 있다.
BFS는 위 두 기준만 적절히 설정한다면 이와 유사한 문제를 마찬가지로 해결할 수 있다.
'iOS 일반 > iOS' 카테고리의 다른 글
| iOS에서의 Audio Session (5) | 2021.06.03 |
|---|---|
| Data Flow Through SwiftUI (2) | 2020.02.25 |
| Swift로 그래프 탐색 알고리즘을 실전 문제에 적용해보기 - DFS 편 (1) | 2020.01.07 |
| Swift로 작성해보는 기본 자료구조 - Stack, Queue (0) | 2020.01.06 |


